Graphes

Définition :

Un graphe est composé de sommets et d'arêtes (ou arcs) reliant certains de ces sommets.

Exemple :
Le diagramme ci-dessous représente un graphe comportant 4 sommets et 5 arêtes.

Ordre d'un graphe :

- L'ordre d'un graphe est le nombre de sommets de ce graphe.
- Le degré d'un sommet est le nombre d'arêtes dont ce sommet est une extrémité.
- Deux sommets reliés par une arête sont adjacents.

Exemple:
- Le graphe représenté ci-dessus est d'ordre 4.
- Le degré du sommet B est 3. Celui de C est 4 (la boucle compte 2 fois).
- A et B sont adjacents. A et D ne le sont pas.

Chaîne :

Une chaîne (ou un chemin) est une suite de sommets telle que chaque sommet est relié au suivant par une arête.
La longueur d'une chaîne est le nombre d'arêtes composant cette chaîne.

Exemple :

(A; B; C; D) est une chaîne de longueur 3.

Cycle :

Un cycle est une chaîne fermée (c'est à dire dont l'origine et l'extrémité sont identiques) dont toutes les arêtes sont distinctes.

Exemple :

(B; C; C; D; B) est un cycle.

Graphe est connexe :

On dit qu'un graphe est connexe si deux sommets quelconques peuvent être reliés par une chaîne.

Remarque:
Intuitivement, cela signifie que le graphe comporte un seul "morceau"

Chaînes et cycles eulériens :

Une chaîne eulérienne est une chaîne qui contient une fois et une seule chacune des arêtes du graphe.
Si cette chaîne est un cycle, on parle de cycle eulérien.

(A; B; C; C; D; B) est une chaîne eulérienne.
Ce graphe ne contient aucun cycle eulérien.
Remarque :
Un graphe connexe contient une chaîne eulérienne si et seulement si on peut le tracer "sans lever le crayon". Le théorème d'Euler (ci-dessous) permet de déterminer facilement ce type de graphe.
On ne peut jamais tracer un graphe non connexe sans lever le crayon !

Théorème d'Euler.

Un graphe connexe contient une chaîne eulérienne si et seulement si il possède 0 ou 2 sommets de degré impair.
Un graphe connexe contient un cycle eulérien si et seulement si il ne possède aucun sommet de degré impair (autrement dit tous ses sommets sont de degré pair)

Exemple :

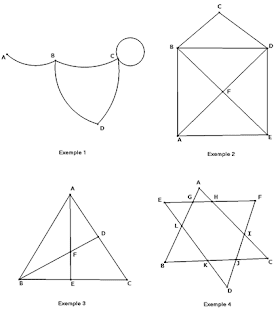
- Dans l'exemple 1, il y a deux sommets de degré impair (A:1 et B:3). Le graphe contient une chaîne eulérienne, par exemple (A; B; C; C; D; B) mais pas de cycle eulérien.
- Dans l'exemple 2, il y a deux sommets de degré impair (A:3 et E:3). Le graphe contient une chaîne eulérienne, par exemple (A; F; D; B; F; E; D; C; B; A; E) mais pas de cycle eulérien.
- Dans l'exemple 3, il y a 4 sommets de degré impair (A:3, B:3, D:3 et E:3). Le graphe ne contient pas de chaîne eulérienne.
- Dans l'exemple 4, tous les sommets sont de degré pair . Le graphe contient un cycle eulérien, par exemple: (G; A; H; F; I; C; J; D; K; B; L; E; G; H; I; J; K; L; G).

Coloration :

Colorier un graphe c'est associer à tout sommet une couleur telle que deux sommets adjacents n'aient pas la même couleur.
Le plus petit nombre de couleurs nécessaire pour colorier un graphe s'appelle le nombre chromatique du graphe.

Exemple :

Le graphe ci-dessus a été colorié a l'aide de 3 couleurs différentes. Il n'est pas possible de le colorier avec seulement 2 couleurs. Le nombre chromatique du graphe est donc 3.

Théorème :

Le nombre chromatique d'un graphe est inférieur ou égal à $\ d_{max}$+1 où $\ d_{max} est le plus grand degré des sommets.

Exemple :

Dans l'exemple précédent le plus grand degré est 4. Le nombre chromatique du graphe est donc inférieur ou égal à 5 (On a vu que c'était 3).


Graphes : une théorie très urbaine :
 Imaginée il y a 250 ans par Euler pour décrire un parcours dans la ville de Königsberg, la théorie des graphes a connu une multitude d'applications pratiques. Elle revient à ses premières amours, au service de l'urbanisme.
Philippe Pajot